题解 |「Codeforces Gym 101173B」Bipartite Blanket | 霍尔定理 / 婚姻配对问题
题解 |「Codeforces Gym 101173B」Bipartite Blanket | 霍尔定理 / 婚姻配对问题

本篇文章汇集了若干网络资料,更加方便查看
题目链接
题意
在一张给定的 n × m 的二分图(带点权)中,有多少完美匹配子集满足权值和大于等于 t
概念:完美匹配
如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。
显然,完美匹配一定是最大匹配 (完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突),但并非每个图都存在完美匹配。
匹配:在图论中,一个「匹配」是一个边的集合,其中任意两条边都没有公共顶点。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
题解
思路
注意到:如果属于 X 的一个点集 V1 属于某个完美匹配,同时属于 Y 的一个点集 V2 也存在于完美匹配中,那么 V1 + V2 一定也属于某个完美匹配。
分别枚举 X 和 Y 中的状态,根据霍尔定理,判断所有点集是不是属于某个完美匹配,最后一起统计。
代码
完整代码见 这里
C int N = 20;
C int _U = N + 1;
C int U = N + 5;
C int SIZE = 1 << _U;
int n, m, t;
int wx[U], wy[U];
int cover_x[SIZE], cover_y[SIZE], cnt[SIZE];
bitset<SIZE> fx, fy;
vector<int> x, y;
inline void solve(int n, int *wx, int *cover_x, bitset<SIZE> &fx, vector<int> &x)
{
for (R int s = 0; s < (1 << n); s++)
{
fx[s] = 1;
int sum = 0;
for (R int i = 0; i < n; i++)
{
if (s & (1 << i))
{
cover_x[s] |= cover_x[s ^ (1 << i)];
sum += wx[i];
fx[s] = fx[s] & fx[s ^ (1 << i)];
}
}
if (fx[s] && cnt[s] <= cnt[cover_x[s]])
{
x.emplace_back(sum);
}
else
{
fx[s] = 0;
}
}
}
char str[U];
inline void init()
{
for (R int s = 0; s < (1 << 20); s++)
{
cnt[s] = cnt[s >> 1] + (s & 1);
}
}
int main()
{
init();
io::read(n, m);
for (R int i = 0; i < n; i++)
{
scanf("%s", str);
for (R int j = 0; j < m; j++)
{
if (str[j] == '1')
{
cover_x[1 << i] |= (1 << j);
cover_y[1 << j] |= (1 << i);
}
}
}
io::readln(wx, wx + n);
io::readln(wy, wy + m);
io::read(t);
solve(n, wx, cover_x, fx, x);
solve(m, wy, cover_y, fy, y);
sort(x.begin(), x.end());
ll ans = 0;
for (const auto &val : y)
{
ans += x.end() - lower_bound(x.begin(), x.end(), t - val);
}
io::writeln(ans);
}
霍尔定理
内容
假设:
- 我们有 1 - N 号女嘉宾,和 1 - N 号男嘉宾。
- 每个女嘉宾在属于自己的小卡片上写下中意的男嘉宾们的号码(没有数量限制,甚至可以全写)。
- 把这些小卡片收集起来。
通过收集的小卡片来判断,是否存在一种配对,使得所有女嘉宾都选到自己中意的男嘉宾。
为了实现这样的配对,我们注意到以下这个事实:
假如任取 k 个女嘉宾,把她们的卡片合起来,这些卡片上写到的所有男嘉宾个数(重复的只算一次)必须至少是 k,否则这些女嘉宾们就会抢起来,就不存在配对。
而霍尔定理是说,如果上面这个事实对于所有的非空女嘉宾子集都满足了,则一定存在一种配对。
证明

已缓存 - http://faculty.wwu.edu/sarkara/hall.pdf
奇妙推论
假设两边的点集分别为 X,Y,则二分图的最大匹配数为 |X| - max{|W| - N(W)},其中 W 是 X 的子集
对于一些特殊的题目,它可以免去建图而直接求最大匹配
来自 Hall定理 二分图完美匹配 - dummyummy - 博客园
二分图G中的两部分顶点组成的集合分别为X, Y(假设有|X| ≤ |Y|)。G中有一组无公共点的边,一端恰好为组成X的点(也就是存在完美匹配)的充分必要条件是:X中的任意k个点至少与Y中的k个点相邻,即对于X中的一个点集W,令N(W)为W的所有邻居,霍尔定理即对于任意W,|W| ≤ |N(W)|
婚姻配对问题
现在有 N 位男生 和 N 位女生,每个男生 都对 N 个女生 的喜欢程度做了排序,每个女生 都对 N 个男生 的喜欢程度做了排序,现在需要确定一个稳定的约会状态。
稳定的定义 如果 男生 i 和 女生 a 牵手,男生 j 和 女生 b 牵手,但 男生 i 更喜欢 女生 b,而 女生 b 发现,相比自己的 男朋友 j,她更喜欢 男生 i,则没有力量阻碍 男生 i 和 女生 b 的私奔,这即是不稳定的。如果不存在如上的情况,则称为稳定。
如何解决
1962 年,美国数学家 David Gale 和 Lloyd Shapley 发明了一种寻找稳定婚姻的策略。不管男女各有多少人,不管他们各自的偏好如何,应用这种策略后总能得到一个稳定的婚姻搭配。换句话说,他们证明了稳定的婚姻搭配总是存在的。有趣的是,这种策略反映了现实生活中的很多真实情况。
在这种策略中:
- 男人将一轮一轮地去追求他中意的女子
- 女子可以选择接受或者拒绝她的追求者
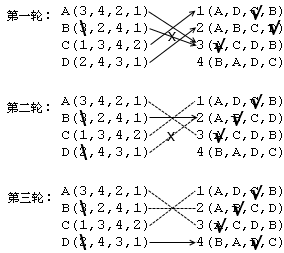
第一轮,每个男人都选择自己名单上排在首位的女人,并向她表白。
此时,一个女孩儿可能面对的情况有三种:
- 没有人跟她表白
- 只有一个人跟她表白
- 有不止一个人跟她表白
女孩的应对策略:
- 在第一种情况下,这个女孩儿什么都不用做,只需要继续等待
- 在第二种情况下,接受那个人的表白,答应暂时和他做男女朋友
- 在第三种情况下,从所有追求者中选择自己最中意的那一位,答应和他暂时做男女朋友,并拒绝其他所有的追求者
第一轮结束后,有些男人已经有女朋友了,有些男人仍然是单身。
在第二轮追女行动中,每个单身男都从所有还没拒绝过他的女孩中选出自己最中意的那一个,并向她表白,不管她现在是否是单身。
和第一轮一样,女孩儿们需要从表白者中选择最中意的一位,拒绝其他追求者。
注意,如果这个女孩儿已经有男朋友了,当她遇到了更好的追求者时,她必须拒绝掉现在的男友,投向新的追求者的怀抱。
这样,一些单身男人将会得到女友,那些已经有了女友的人也可能会被甩掉,重新变成光棍。
在以后的每一轮中,单身的男人继续追求列表中的下一个女孩儿,女孩儿则从包括现男友在内的所有追求者中选择最好的一个,并对其他人说不。
这样一轮一轮地进行下去,直到某个时候所有人都不再单身,下一轮将不会有任何新的表白发生,整个过程自动结束。此时的婚姻搭配就一定是稳定的了。
正确性
这个策略会不会像之前的修补法一样,出现永远也无法终止的情况呢?不会。
下面我们将说明,随着轮数的增加,总有一个时候所有人都能配上对。
由于在每一轮中,至少会有一个男人向某个女人告白,因此总的告白次数将随着轮数的增加而增加。
倘若整个流程一直没有因所有人都配上对了而结束的话,最终必然会出现某个男人追遍了所有女孩儿的情况。
而一个女孩儿只要被人追过一次,以后就不可能再单身了。
既然所有女孩儿都被这个男人追过,就说明所有女孩儿现在都不是单身,也就是说此时所有人都配上对了。
接下来,我们还需要证明,这样得出的配对方案确实是稳定的。
首先注意到,随着轮数的增加,一个男人追求的对象总是越来越糟,而一个女孩儿的男友只可能变得越来越好。
假设 男 A 和 女 1 各自有各自的对象,但比起现在的对象来,男 A 更喜欢 女 1。因此,在此之前 男 A 肯定已经跟 女 1 表白过。既然 女 1 最后没有跟 男 A 在一起,说明 女 1 拒绝了 男 A,也就是说她有了比 男 A 更好的男人。
这就证明了,两个人虽然不是一对,但都觉得对方比自己现在的伴侣好,这样的情况绝不可能发生。
参考资料
为了防止出现参考资料 404 或原网站响应迟缓的情况,所有参考资料均转为
GitHub并由jsDelivr分发
指向原始内容的链接可见脚注
部分参考资料散落在文中,请谅解