题解 | CF930 / Codeforces Round 468 (Div. 1)
题解 | CF930 / Codeforces Round 468 (Div. 1)

未独立完成的题目
- C
- E
A
题意
有一棵苹果树,每个点都有一个苹果。每秒,不在根上的苹果会向根移动一步,在根上的苹果会被加进答案。每个点上的苹果数量每秒会对 2 取模。问答案是多少。
题解
如果没被消耗掉的话,相同深度的苹果肯定同时到达根节点。只要统计下某个深度有几个苹果,把每个深度的苹果数对 2 取模后加起来就是答案。
总结
签到题。
B
题意
小 K 创建一个由小写英文字母构成的字符串 S,并把这个字符串告诉小 V。然后小 K 在 [0,\operatorname{len}(S)] 的范围内任取一个整数 k,把 S 的前 k 个字符移到末尾。然后小 K 会告诉小 V 新串的首字母,小 V 还可以让小 K 告诉他新串中一个位置 p 的字母(位置由小 V 决定)。如果小 V 以最优策略提问,他有多少概率可以唯一确定 k。
题解
对每个字母在原串中出现的位置进行统计。对相同字母开头的情况,枚举位置 p,统计有多少个串能被唯一确定下来,取个 max 就是新串以这个字母开头的答案。
总结
考场做出,重做时独立完成。
C
题意
小 T 有 n 条线段,每条线段的端点都是在 [1, m] 之间的正整数,他发现不存在一个整点被所有线段覆盖。现在小 S 想验证这个事实。小 S 可以问小 T 某个整点被多少条线段覆盖这样的问题。求一个最大的集合 S,使得在小 S 问完 S 中的所有点之后仍不能验证这个事实。
题解
题意比较难懂。考虑 x, y, z 三个点,当且仅当 \operatorname{ask}(y) 小于 \operatorname{ask}(x) 且 \operatorname{ask}(y) 小于 \operatorname{ask}(z),说明有部分线段过不了 y 这个点,即不存在一个整点被所有线段覆盖。要破坏这个条件,转化一波就是求 \operatorname{ask}(x)) 的最长先上升后下降子序列。\operatorname{ask}(x) 可以通过差分 O(n) 处理。可以用树状数组处理出每个点到开头的最长不降子序列和到末尾的最长不升子序列,然后拼起来即可。
总结
考试的时候没看懂题意,这次参考题解才想出来。
D
题意
在一张棋盘上有 n 个黑棋和 1 个白棋,棋子可以往上 / 下 / 左 / 右移动,但是不能和别的棋子重合。白棋先走,如果白棋能不被黑棋堵牢,则白棋赢。给你黑棋坐标,问有多少种白棋的起始位置使得黑棋会赢。
题解
考虑一枚黑棋怎么堵住白棋的一个方向。如图,黑棋可以限制白棋不能继续往右走。
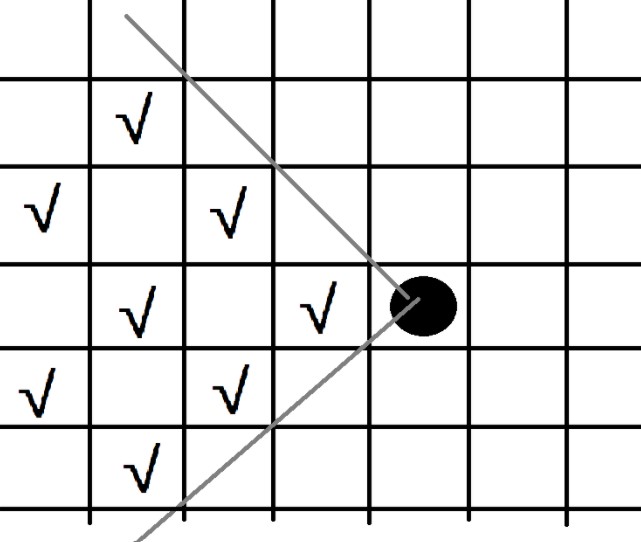
黑棋和白棋横坐标之差为奇数,纵坐标之差为偶数。在纵坐标相同前黑棋只要一直和白棋反着走,纵坐标相同,横坐标差 1 后就可以一直顶着白棋了。一颗黑棋可以控制白棋的一个方向,所以要四颗黑棋才能控制一颗白棋。问题转化成“有多少个位置可以四个方向都被黑棋控制”。
可以通过旋转坐标系的办法降低实现难度。
总结
思想还记得,细节不记得。
E
题意
有 k 个硬币,每个硬币可以正面朝上 / 反面朝上。
限制条件形如 (l_i,r_i)。前 n 个限制条件要求区间 [l_i,r_i] 至少一个硬币正面朝上,后 m 个限制条件要求区间 [l_i,r_i] 至少一个硬币反面朝上。
题解
对关键点离散化后考虑 DP,f[i][0/1] 表示考虑第 i 及之后的关键点,disc[i] \sim disc[i + 1] 中含有 0/1 的方案数的后缀和。g[i] 表示 disc[i] \sim disc[i + 1] 中同时有 0 和 1 的方案数。min[0/1][i] 表示限制条件为 0/1,i 右侧最近的,对应左端点不在 i 左侧的右端点。
答案为 g[0]。
总结
未独立完成。