题解 | 2015 ACM-ICPC World Finals - Marrakech
题解 | 2015 ACM-ICPC World Finals - Marrakech

A
题意
定义 \operatorname{price}(k)=p\cdot(\sin(a\cdot k+b)+\cos(c\cdot k+d)+2),其中 p,a,b,c,d 是给定的参数。序列 S=[\operatorname{price}(1),\operatorname{price}(2),...,\operatorname{price}(n)],求 \max\limits_{1\le i\le j\le n} {S_i-S_j}。
题解
能成为答案 S_i 的只有前缀最大值,答案的 S_j 则是 S_i 和下一个前缀最大值之间的最小值。从前往后扫一遍即可。
B
C
题意
有一家装备出租公司收到了按照时间顺序排列的 n 个请求。
这家公司有 k 个搬运工。每个搬运工可以搬着一套装备按时间顺序去满足一些请求。一个搬运工从第 i 个请求的位置把东西搬到第 j 个请求的位置需要一些费用。公司的编号是 1,请求的编号是 2\sim n+1。所有搬运工必须从公司出发。
求满足所有请求所需的最小搬运费用。
题解
- S\rightarrow 1 连一条流量为 [0,k],费用为 0 的边
- 2\sim n+1 拆成两个点 u_i,v_i,u_i 和 v_i 间连一条流量为 [1,1],费用为 0 的边
- v_i\rightarrow T 连一条流量为 [0,1],费用为 0 的边
- 1\rightarrow u_i 连一条流量为 [0,1],费用为 dis_{1,i} 的边
- v_i\rightarrow u_j(i\lt j) 连一条流量为 [0,1],费用为 dis_{i,j} 的边
然后使用有源点上下界可行流。
D
题意
一块正方形的奶酪上有 n 个球形的孔,孔间不重叠。想要在竖直方向上把这块奶酪切成 s 片重量相等的奶酪,问每片奶酪的厚度是多少。
题解
球的体积公式是 \frac 4 3\pi\cdot R^3。球缺体积公式是 \pi\cdot h^2\cdot(R-\frac h 3) 或 \frac 1 6\pi\cdot h\cdot(3r^2+h^2),其中 R 是球体半径,h 是球缺的高,r 是球缺底面的半径。
直接二分当前奶酪的厚度,用上面两个公式算孔的体积即可。
E
题意
给你 n 个字符集为 \{A,C,M\} 的字符串,你需要将其分成 2 列,使得每列种相邻的字符串前一个是后一个的子序列,且每列的最后一个字符串都是一个给定字符串 s 的子序列。
题解
如果这 n 个字符串中有字符串不是 s 的子序列,显然 impossible。
否则,先对字符串按照长度排序。维护两列 f,g。现在加入一个字符串 str,分三类讨论。
- 如果既不能加入 f 也不能加入 g,则
impossible - 如果既能加入 f 也能加入 g,对于这种字符串,我们将其放入一个备胎序列 t。要求 t 中的串满足既能接在当前的 f 后面,也能接在当前的 g 后面。如果 t 非空且 str 不能能接在 t 后面,就让 str 和 t 接在 f,g 后面
- 如果只能加入 f 或 g 中的一个,就把 str 接在该串后面,t 接在另一串后面
F
题意
给定一个 r 行 c 列的虚拟键盘,通过上 / 下 / 左 / 右 / 选择共 5 个控制键,你可以移动屏幕上的光标来打印文本。
一开始,光标在键盘的左上角,每次按方向键,光标总是跳到下一个在该方向上与当前位置不同的字符,若不存在则不移动。每次按选择键,则将光标所在位置的字符打印出来。
现在求打印给定文本(要在结尾打印换行符)的最少按键次数。
题解
这题只要爆搜 + 剪枝就行。
首先预处理从每个位置往上 / 下 / 左 / 右跳一格会到哪里,然后大力 BFS。剪枝时可以设 vis_{x,y} 表示经过位置 (x,y) 时最多能匹配到文本串上的哪个位置,转移时如果发现匹配到的位置没有增加,就不用转移(正确性显然)。
G
H
题意
坎儿井是一种灌溉系统,由一条地下的水源和若干条竖直的井组成。
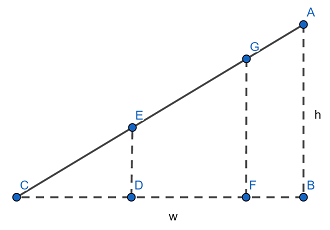
本题中,将其抽象为如上模型。
其中 A\rightarrow B 和 B\rightarrow C 这两条井必须挖。还要在中间挖 n 条竖井。竖井的横坐标可以是 [0,w] 中的任意实数。挖出来的土必须要送到 AC(地面)上,每个位置的土可以沿水平方向及竖直方向任意运输,代价即为最短距离。要求你合理安排这 n 条竖井的位置,使得总代价最小。
I
题意
一条河分为东西方向的 n 条航道(1\le n\le 10^5),每条航道宽为 w。
有一个点从 [t_1,t_2] 间的某个时间从河岸上的某处(后称原点)出发,以匀速 v 从南向北横穿这个游泳池。第 i 条航道(i\in\{0,1,2,...,n-1\})中有 m_i 条船,沿东 / 西以速度 u 匀速移动,初始时其船首相对于过原点南北方向的这条直线的距离是 p_{i,j},船的长度为 l_{i,j}。要求点从到达第 i 条航道到离开为止,不可以有船穿过这条南北方向的分界线。
求最长的可行出发时间区间的长度。
题解
每条船的信息可以转化为一个 [l_i,r_i) 这段时间内不能出发的限制条件。
具体来说,对于第 i 条航道内长度为 l 的船,船头到达这条直线的时刻为 \frac p u,船尾离开这条直线的时刻为 \frac {p+l} u,\frac p u\sim\frac {p+l} u 这段时间内点都不能在航道内。考虑两种极限合法情况,即船头到达直线时点正好离开这个区间,船尾离开直线时点正好进入这个区间。所以点不能在 \frac p u-\frac{w\cdot(i+1)}v\sim\frac{p+l}u-\frac{w\cdot i}v 这段时间内出发。
所以直接差分即可。
J
题意
对于一定长度和宽度的长方形方格纸,在四条边上(不包括角落)选四个点按顺序连成平行四边形。n 次询问,问面积在 a_l 到 a_r 之间的平行四边形中,哪种面积平行四边形数量最多。
题解
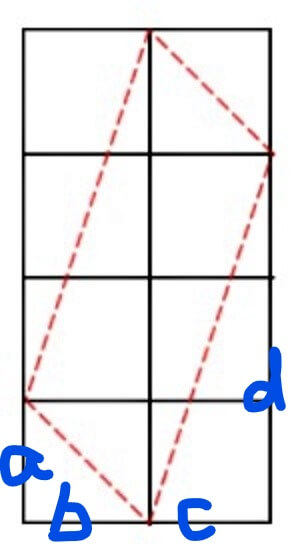
平行四边形的面积等于外面矩形的面积减去四个小三角形的面积。
设 d(x) 表示 x 的因数个数,ans(x) 表示面积为 x 的平行四边形的数量。则 ans(x)=\sum\limits_{i+j=x}d(i)\cdot d(j)。这显然是一个卷积的形式,直接上 FFT。
K
题意
给一张简单图 G,至少包含一个环。找到所有的整数 k,使得 G 中的边可以染成 k 种颜色,并且所有简单环中的 k 种颜色的边的数量都相同。
题解
结论题。忽略图中的桥边(这些边显然不会对答案造成影响),对于每条剩下的边 i,计算去掉 i 后新产生的桥边的数量 w_i,答案为所有 w_i+1 的 \gcd。可以参考证明 ᴮᵃᶜᵏᵘᵖ。
L
题意
考虑 4 种天气晴 / 多云 / 雨 / 雾,已知每种天气出现的概率分别为 p_\text{sunny},p_\text{cloudy},p_\text{rainy},p_\text{frog}。现在要传输未来 n 天的天气情况。想要对这 4^n 种可能的天气情况进行二进制编码,并且不存在一个天气情况的编码是另一个编码的前缀。问期望编码长度最小是多少。
题解
哈夫曼编码。对出现概率相同的情况压到一起计算。