题解 | CF521 / Codeforces Round 295 (Div. 1)
题解 | CF521 / Codeforces Round 295 (Div. 1)
未独立完成的题目
- 521E
A
题意
字符集为 \{A,T,C,G\}。给定一个长度为 n 的字符串 S,问有多少种方案构造一个字符串 T 使得 S,T 在移位过程中相同的位数的总和最大。
题解
不难发现 由于移位,T 中每一个字符产生的贡献就是 S 中和它相同的字符的出现次数。当且仅当 T 中的每一个字符都是 S 中出现次数最多的字符,相同位数的总和最大。于是只要统计下 S 中每个字符的出现次数,设有 x 个字符出现次数最多,答案就是 x^n(T 的每一位可以在这 x 个字符中任选一个)。
总结
需要观察能力。
B
题意
小 V 和小 P 用 m 个方块搭建了一个图形。这些方块的标号为 0\sim m-1。以地面为 x 轴,垂直向上为 y 轴正方向,建立直角坐标系。用每个方块左下标的坐标表示它的位置。每个方块的坐标都是整数。
题解
按照题意,因为 m 进制数每一位的位权为 m,所以两人的策略都是简单贪心。小 V 需要移除当前能移除的最大值,小 P 需要移除当前能移除的最小值。可以维护一个当前可删除的方块的集合。每次删除一个方块,就触发区块更新,判一下周围的 5\times 5 的方块的可删除性,然后更新集合。
总结
思维简单的大模拟。
C
题意
给定一个 n 位的十进制数 a_1a_2...a_n,在数字之间加 k 个 +,得到一个式子。求每种方案的式子的运算结果之和。
题解
考虑每一个 a_i 对答案的贡献,这和 a_i 后最近的 + 的位置有关。
- 如果 + 在 a_i 后面,则 a_i 本身的贡献是 10^0\times a_i,剩下的 + 的摆法有 \binom {n-2} {k-1} 种,贡献是 10^0\times a_i\times\binom {n-2} {k-1}
- 如果 + 在 a_{i+1} 后面,则 a_i 本身的贡献是 10^1\times a_i,剩下的 + 的摆法有 \binom {n-3} {k-1} 种,贡献是 10^1\times a_i\times\binom {n-3} {k-1}
- 如果 + 在 a_{i+2} 后面,则 a_i 本身的贡献是 10^2\times a_i,剩下的 + 的摆法有 \binom {n-4} {k-1} 种,贡献是 10^2\times a_i\times\binom {n-4} {k-1}
以此类推,注意到 a_i 离 + 距离相同时,乘上的组合数相同,可以把它们一起计算。于是有
D
题意
给定 k 个正整数 a_1,a_2,...,a_k。
有 n 个操作,每个操作给定三个参数 t,i 和正整数 b。
- t=1,将 a_i 赋值为 b
- t=2,将 a_i 加上 b
- t=3,将 a_i 乘上 b
可以从这 n 个操作中选出最多 m 个操作执行,并且可以钦定操作顺序,目标是最大化 \prod_{i=1}^{k} a_i。
题解
首先如果确定了选择的操作,操作顺序肯定是先赋值,再加法,最后乘法。
因为选择的赋值操作不能把 a_i 变小,所以可以把赋值转换成加法。然后注意到对于同一个 i 的所有加法应该从大到小贪心地执行,于是可以把加法转化成乘法。最后再对转化出的乘法排个序,就得到了应该执行哪些操作。
总结
简单贪心。
E
题意
给定一张 n 个点 m 条边的简单无向图,问图中能否找到两个点,满足这两个点之间有至少三条完全不相交的简单路径。
题解
这是样例 1,2 的图,其中红色的边是其生成树。
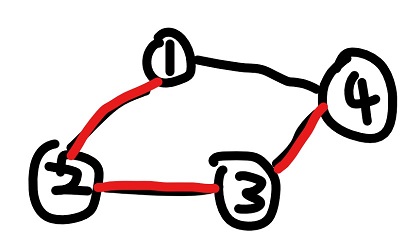
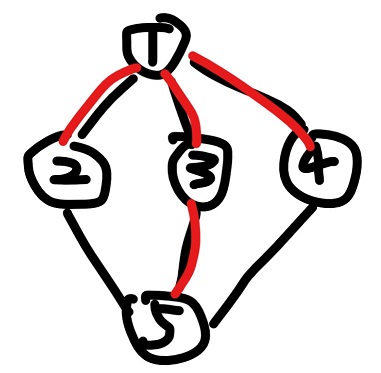
观察发现,如果存在两个环有边相交,就存在符合题意的两个点。因为我们可以取相交这段的起点和终点作为 u,v,然后就存在三条路径了。从生成树的角度,如果存在一条树边被两条非树边覆盖,就存在答案。
现在对于每个连通块 DFS 一遍。对每条非树边 (a,b) 都暴力标记被它覆盖的树边。如果发现之前这个树边被非树边 (c,d) 标记过,那么可以直接通过 (a,b) 和 (c,d) 获取答案。
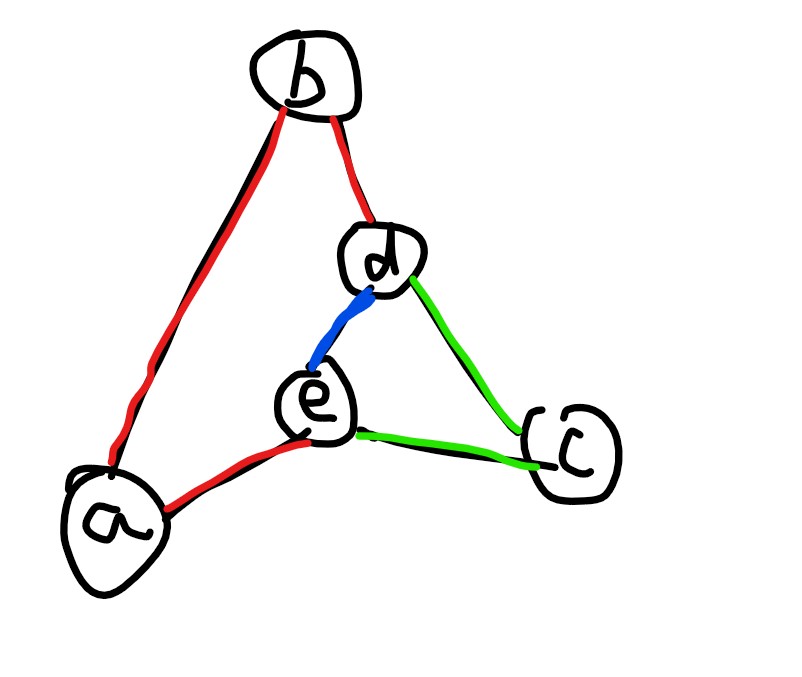
我们钦定 dep_b\gt dep_a,dep_d\gt dep_c,且 d 为 b 的祖先。设 e=\operatorname{LCA}(a,c),则三条路径分别为 d\rightarrow e,d\rightarrow b\rightarrow a\rightarrow e,d\rightarrow c\rightarrow e。找路径的实现上暴力跳 fa 即可。
总结
构造题。