题解 | CF297 / Codeforces Round 180 (Div. 1)
题解 | CF297 / Codeforces Round 180 (Div. 1)
未独立完成的题目
- C
- E
A
题意
给你两个 01 串 a, b,定义 parity(str): 如果 str 中有奇数个 1,返回 1,否则返回 0。有两种操作
- 把 parity(a) 附到 a 的最后
- 在 a 的前面删掉一个数
可以执行任意步操作,问你是否可以把 a 变成 b。
题解
注意到如果 a 中有偶数个 1,则 1 的数目不可能增多(如果 a 中有奇数个 1,可以先在后面添上一个 1,之后 1 的数目就不可能增多了)。并且通过合适的策略,可以把 a 变成任何一个 1 的数目小于等于它的 01 串。只要数一下 a, b 中 1 的数目即可。
总结
这题考场 AC,并且重新思考时独立完成。
B
题意
有 k 种🐟,每种🐟都有一个重量,并且它们按照重量从小到大排序后有一个编号。Alice 手上有 n 条🐟,Bob手上有 m 条🐟。给出 Alice 和 Bob 手上鱼的编号,问 Alice 手上的🐟的总重是否可以大于 Bob。
题解
首先把这些编号离散化一下,再做个后缀和。从后往前扫,如果某个位置 Alice 手上的🐟的数量大于 Bob 了,我们就把这之后的🐟的重量全赋成 INF,这之前的全赋成 1。这样 Alice 手上的🐟的重量肯定大于 Bob。
总结
这题考场 AC,并且重新思考时独立完成。
C
题意
有一个数组 s,包含 n 个互不相同的非负整数。让你分成两个数组 a, b。使得
- a_i,b_i 为非负整数
- s_i=a_i+b_i
同时,要求 a, b 中重复出现的数分别不超过 \lceil \frac n 3 \rceil。
题解
构造。把 s 数组排序后,
- a 数组的前 \frac 1 3 填 1\sim \frac n 3,b 数组对应填。
- b 数组的中间 \frac 1 3 填 \frac n 3 \sim \frac{2n} 3,a 数组对应填
- b 数组的最后 \frac 1 3 填 n-i-1,a 数组对应填。
这样保证了 a 数组的前面和后面是两两不同的,b 数组的中间和后面是两两不同的。
总结
这题还记得是分三段构造,但是构造策略没想出来,未独立完成。
D
题意
用 k 种颜色拼成一个 h*w 的地毯,同时对于每一对有公共边的方块给定了一个限制条件,要求它们同色或者不同色。这些限制条件只要满足 3\over 4 即可。如果可以构造,给出一种方案。
题解
这题给了 k 个颜色,实际上对于 k\ge 2 的情况,只要两个颜色就可以了,并且总是可以构造。对于k=1 的情况简单判一下 E 的数量是否超过总数的 3\over 4。否则,注意到有 h*(w-1)+w*(h-1) 个限制条件,我们先满足 h*(w-1) 和 w*(h-1) 中较大的限制条件,再在剩下的条件中挑一部分满足。可以先翻转一下,保证 h\le w。然后行内全满足,上下的关系总可以满足一半以上(先钦定第一个块的颜色,如果发现这样填下来满足不了一半,把整行颜色反转,就可以满足一半以上了),加起来超过总数的 3\over 4。
总结
独立完成。
E
题意
一个环上有 2n 个顶点。要求选择 3 条不重复的弦,在它们顶点处建 6 个熊洞,且每条弦的两个端点的距离(距离的定义是在环上经过的熊洞数,取较小值)相同,询问其方案数。
题解
三条弦总共有五种关系,其中 2, 5 是合法的。
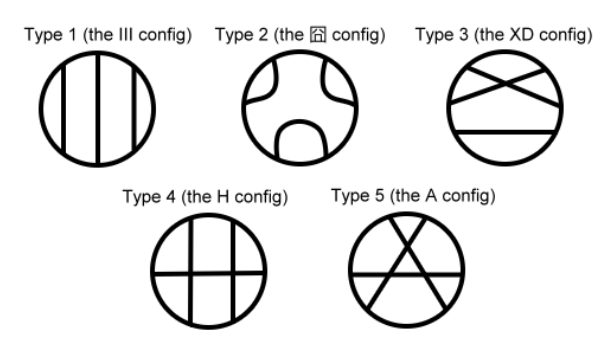
但是 2, 5 的方案比较难算,考虑从总方案中减掉 1, 3, 4 的方案。
假设我们能处理出每条弦的左边和右边弦的数量,记为 L_i, R_i,对于类型 1,答案就是 \sum L_i \cdot R_i。把类型 3 和类型 4 一起计算。它们的共同点是从两条弦(对于类型 3 是顶上两条,对于类型 4 是竖着的两条)的角度观察,一条弦和自己相交,一条线和自己相离。那么情况数就是 \sum (L_i + R_i)*(n-L_i-R_i-1)\over 2(每种情况会被计算两次)。
现在问题是怎么计算 L_i,R_i。设以弦 (x_i,y_i) 的角度观察(x_i\lt y_i),如果弦 (x_j,y_j) 在自己左边(x_j\lt y_j),则 x_j\lt x_i,y_j\gt y_i \ or \ y_j \lt x_i 或者 y_j\gt x_j\gt y_i,。否则,x_i\lt x_j\lt y_j\lt y_i。这可以用二维偏序解决。复杂度 n \log n。
总结
未独立完成。