博弈论学习笔记
博弈论学习笔记
三条定理
有个叫博弈图的东西,把每个状态看作一个点,把它向它能推到的状态连边,如下图。
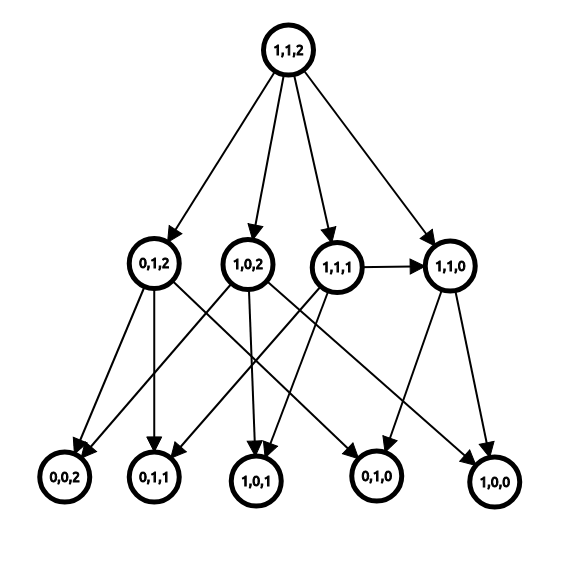
定义
- 必胜状态: 先手必胜的状态
- 必败状态: 先手必败的状态
则有
- 没有后继状态的状态是必败状态
- 一个状态是必胜状态,当且仅当它的至少一个后继状态是必败状态
- 一个状态是必败状态,当且仅当它的所有后继状态是必胜状态
其实很好理解
- 玩不下去了,就败北了
- 如果至少一个后继状态是必败的,那么只要往这个状态走,对面就必败了
- 如果后继的所有状态都是必胜的,不管怎么走,对面都躺赢
从这个开始会不会感觉好一点,为什么其它文章都是从 Nim 游戏引入的,让人丧失自信心
Nim 游戏
n 堆物品,每堆 a[i] 个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。取走最后一个物品的人获胜。
Nim 和
有一个神秘结论,计算每堆物品个数的异或和 a[1] ^ a[2] ^ ... ^ a[n](这玩意又叫 Nim 和),如果这个数为 0,当前状态必败,否则必胜。
证明
我们试图证明。参照上面的三个定理,我们只要说明以下两句话的正确性,就可以证明了。
- 如果一个状态 Nim 和不是 0,我们一定有办法把它做到 Nim 和为 0
- 如果一个状态 Nim 和是 0,那么它要么没有后继状态,要么所有后继状态 Nim 和都不是 0
(由于物品个数单调递减,最后肯定会被取完,所以只要能让对手的 Nim 和保持 0,就稳了)
首先,异或和不是 0,意味着把这些数二进制排列后,如图
| 堆的大小 | 第 3 位 | 第 2 位 | 第 1 位 | 第 0 位 |
|---|---|---|---|---|
| 7 | 0 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 |
这组数据的 Nim 和是 13。
在 Nim 和的最高位这一列(设为 k)上,肯定有奇数个 1。把第 k 位 1 的任意一个数拎出来,与 Nim 和异或下,再放进去,这样保证了
- 这个数与 Nim 和的异或结果肯定小于这个数(本来这个数至少是二进制下的 k 位数,现在至多 k - 1 位)
- Nim 和为 0(异或自身为 0)
我们挑选 15 这个数,异或上 13,可以得到一个 Nim 和为 0 的表。
| 堆的大小 | 第 3 位 | 第 2 位 | 第 1 位 | 第 0 位 |
|---|---|---|---|---|
| 7 | 0 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
如果一个状态的 Nim 和为 0,那每个位置都有偶数个 1。最简单的情况是这些位置全是 0,这样就输了。如果不是这种情况,由于只能取一堆,而且不能不取,这样无论取(同一行)哪些位置的 1,都把原来某一列的偶数个 1 变成奇数个 1 了。
SG 函数和 SG 定理
mex 函数
我们先定义一个 mex (minimum excludent) 函数,这个函数返回集合中不存在的最小非负整数。例如 mex{0, 1, 5} = 2, mex{2, 3, 4} = 0, mex{} = 0。
SG 函数
定义 SG(x) = mex(S), 其中 S 是 x 所有后继状态 SG 函数值的集合。例如 x 有 3 个后继状态 a, b, c,那么 SG(x) = mex{SG(a), SG(b), SG(c)}。根据 mex 函数的定义,如果 x 没有后继状态,S 是个空集,那么 SG(x) = 0。当且仅当 x 为必败点时,SG(x) = 0。
SG 定理
游戏和的 SG 函数等于各个游戏 SG 函数的 Nim 和。因为 SG(x) = 0 意味着当前必败,假设对于 n 局游戏,起点分别为 S1, S2, ..., Sn,当且仅当 SG(S1) ^ SG(S2) ^ ... ^ SG(n) != 0 时这个游戏先手必胜。这个定理常被用来分治。
取石子问题
有 n 个石子,每次只能取
1, 3, 4个石子,先取完石子者胜利,那么 1 ~ n 的 SG 值为多少?
首先,SG(0) = 0。
(以下建议手推,加强印象)
- x = 1 时,可以取走
{1}个石子,剩余{0}个,所以 SG(1) =mex{SG(0)}= mex{0} = 1 - x = 2 时,可以取走
{1}个石子,剩余{1}个,所以 SG(2) =mex{SG(1)}= mex{1} = 0 - x = 3 时,可以取走
{1, 3}个石子,剩余{2, 0}个,所以 SG(3) =mex{SG(2), SG(0)}= mex{0, 1} = 2 - x = 4 时,可以取走
{1, 3, 4}个石子,剩余{3, 1, 0}个,所以 SG(4) =mex{SG(3), SG(1), SG(0)}= mex{2, 0, 1} = 3 - x = 5 时,可以取走
{1, 3, 4}个石子,剩余{4, 2, 1}个,所以 SG(5) =mex{SG(4), SG(2), SG(1)}= mex{3, 0, 1} = 2 - x = 6 时,可以取走
{1, 3, 4}个石子,剩余{5, 3, 2}个,所以 SG(6) =mex{SG(5), SG(3), SG(2)}= mex{3, 2} = 0 - x = 7 时,可以取走
{1, 3, 4}个石子,剩余{6, 4, 3}个,所以 SG(7) =mex{SG(6), SG(4), SG(3)}= mex{0, 3, 2} = 1 - x = 8 时,可以取走
{1, 3, 4}个石子,剩余{7, 5, 4}个,所以 SG(8) =mex{SG(7), SG(5), SG(4)}= mex{1, 2, 3} = 0
...
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| SG(x) | 0 | 1 | 0 | 2 | 3 | 2 | 0 | 1 | 0 |
所以,我们可以这样计算 SG 函数。
// f: 可改变当前状态的方式,要在 getSG 之前预处理
// SG: 0 ~ n的 SG 函数值
// S: x 后继状态的集合
int f[N], SG[MX];
bitset<MX> S;
void getSG(int n)
{
memset(SG, 0, sizeof(SG));
// 因为 SG(0) 始终等于0,所以 i 从 1 开始
for (int i = 1; i <= n; i++)
{
// 每一次都要将上一状态的后继集合重置
S.reset();
for (int j = 0; f[j] <= i && j <= N; j++)
{
S.set(SG[i - f[j]]); // 将后继状态的 SG 函数值进行标记
}
for (int j = 0;; j++)
{
if (!S.test(j))
{ // 查询当前后继状态 SG 值中最小的非零值
SG[i] = j;
break;
}
}
}
}
威佐夫博弈
游戏规则
参考维基百科
有两堆石子,两个顶尖聪明的人在玩游戏,每次每个人可以
- 从任意一堆石子中取任意多的石子
- 从两堆石子中取同样多的石子
不能取的人输,问谁会获得胜利。
想法
设两堆石子中较小的一堆大小为 a,另一堆大小为 b,并称 (a, b) 这个数对为当前的状态。注意到 Δ = b - a 在第二种操作下不会改变。
列出如下后手必胜的局面(后称奇异状态):
0 01 23 54 76 108 13
奇异状态是没法一步变到更小的奇异状态的状态。比如 1 2 只能变到 0 1 / 0 2 / 1 1,而没法变到 0 0。对于 2 x,可以一步变到 1 2。如果状态 (a, b) 的 a 已经在之前的奇异状态出现过了,那么显然可以通过第一种操作一步转到之前的奇异状态,所以奇异状态中的第一个数一定是之前的奇异状态中没有出现的数。然后如果把 0 0 当成第 0 个奇异状态的话,奇异状态的 b = a + i(这一个可以观察出来)。感性说明下,2 3 / 3 4 / 4 5 这类状态都可以通过第二种操作变成 1 2,但是 3 5 就不行,因为之前的奇异状态没有相差 2 的,4 7 也不行,因为之前的奇异状态没有相差 3 的。
也许可以这样理解:我们把可以通过奇异状态反推一步得到的状态都划掉,留下的就是下一个奇异状态。
快速判定奇异状态
威佐夫的结论是 delta * (sqrt(5) + 1) / 2 = a 时先手必败,否则先手必胜。其中 (sqrt(5) + 1) / 2 是 黄金分割数 + 1。